Improving Search Responsiveness for Large Data Tables
Chris Vaszauskas
Staff Engineer
At AxisCare, we build software for home care agencies. Our agencies serve clients, typically senior citizens who would prefer to remain in their homes, but need some extra assistance around the house. A home care agency hires caregivers, matches them with compatible clients, then schedules visits between the clients and caregivers where the caregiver assists the client with the kinds of tasks that become more difficult as you age – grocery shopping, cleaning, etc.
We expose our data to customers via internal reporting tools. Our largest customers often run reports across huge datasets, then use frontend tools like searching, filtering, and sorting to narrow down the dataset and perform operations on it. For large tables, our frontend search operation was taking quite a bit of time to execute – enough time that users felt the slowness via input latency as they typed into the search field. This is the story of how we improved our search latency by an order of magnitude.
The Starting Point: Check Every Cell
Our original search implementation was the most basic form of table search: given a table and a search term, check every cell, then return rows with a cell that includes the term.
function basicSearch(
columns: Column[],
rows: Row[],
term: string,
): Row[] {
const result = [];
for (const row of rows) {
for (const column of columns) {
const cell = column.render(row).toString().toLowerCase();
if (cell.includes(term)) {
result.push(row);
break;
}
}
}
return result;
}
This function does lots of work. If we want to implement real-time search where search results are processed as the user types, we have to iterate every cell on every keystroke. For small tables, the latency isn’t noticeable. But for large tables, the latency becomes viscerally clear as keystrokes take longer and longer to appear on screen and the application feels slower and slower. We could apply some tricks like debouncing to reduce the perceived search latency. But first, let’s see if we can do anything about the actual latency.
As it happens, there is a time-tested technique to improve performance in software development: Do Less Work. Turns out that doing less work is actually faster than doing more work! But what does “work” mean here? First, let’s define our basicSearch function’s performance more formally.
If we examine the code again, we see that basicSearch is a function of:
- the number of cells (or
rows.length * columns.length) - the cost of
string.includes(which scales with the length of the two input strings)
In big-O notation, our function’s time complexity is:
O(cells * O(string.includes))
So we have two factors influencing the amount of work we do. If we want to Do Less Work, we need to find a way to reduce one of the two factors.
Let’s start with the first: cell count.
Examining the Dataset
Many of our largest reports operate on the Visit entity and include information about the visit, the client, and the caregiver. Here are some example columns that often appear on reports:
- Visit date
- Client name
- Caregiver name
- Visit start time
- Visit end time
- Caregiver clock-in time
- Caregiver clock-out time
- Services provided during the visit
- Bill rate
- Pay rate
- … and other attributes of the visit, the client, or the caregiver
One observation about this dataset is that there is a ton of overlap in the cells. If we run a report over a time period of one year, we may get hundreds of thousands of rows (each representing one visit) and millions of cells. But the number of unique cells is often significantly lower. Take some columns for example:
- Visit date – if we run the report for a year, this column only has 366 possible unique values
- Start/end time – these use minute-level resolution, meaning there are only 1,440 possible unique values
- Client/caregiver – these are bounded by the number of clients and caregivers defined in the system
- Bill/pay rate – agencies often use a standard set of rates across all visits with rare exceptions
All this means the number of unique cells is probably significantly lower than the number of total cells in the table. What if we could run our search function over each unique cell? This would reduce our time complexity from
O(cells * O(string.includes))
to
O(uniqueCells * O(string.includes))
The larger the difference between cells and uniqueCells, the better our search operation scales.
Benchmarking Our Starting Point
Now that we have a theoretical pathway to a faster search, we need to establish a performance baseline. First, we’ll generate a test dataset we can use to verify our performance optimizations. I used faker to generate a dataset based on 10,000 clients with 2 visits a week for one year. I used random times for the time-related fields. I also added one column of completely random data to the table to stress the performance of our new search algorithm (since in theory, it will perform worst on random inputs).
Here are some stats on our test data:
rows: 1,040,000
cells: 8,320,000
uniqueCells: 1,061,658
searchMatches: 297,616
And here’s how our original basicSearch function performs:1
377ms basicSearch()
Ouch. One search operation takes nearly a half-second to complete. Google’s RAIL guidelines recommend budgeting for 50ms to handle user input events like keyboard presses, and we are over-budget by almost 8x – not even accounting for the time our UI framework will need to process the results. If we want to go faster, we’ll have to preprocess our data into an index.
Creating an Index
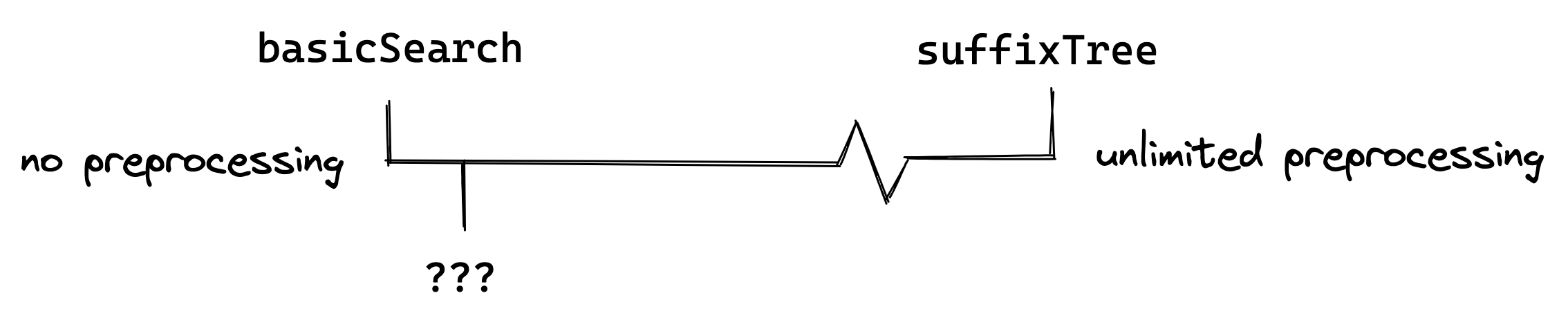
I often joke that the more experience I gain as a developer, the more my job becomes to say “it depends” all day. Like any other performance optimization that involves preprocessing, our indexing strategy is a tradeoff: the index takes time and memory to create, and we trade those resources for a faster search operation. There is a large spectrum of possible indexing strategies. On one side, we have our original basicSearch function that uses zero preprocessing. And on the far opposite side, we have advanced indexing algorithms (like trigram indexes or suffix trees) that enable sub-millisecond matching, but require, erm, significant time and memory to construct. Part of our challenge will be to decide where we want to land on the spectrum. In other words, how fast is fast enough for our search operation? And how much time and memory are we willing to spend to create an index, knowing that our users can’t begin a search operation until the index is complete?
We already know our baseline: the basicSearch function that requires zero preprocessing. Let’s start by taking one step farther along the spectrum with the most basic index possible: a map from unique cells to the containing rows. (Again, we expect this to improve performance because the number of unique cells is significantly lower than the number of total cells.)
Index Attempt #1
First, we need to prepare the index:
function prepareIndex(
columns: Column[],
rows: Row[],
): Map<string, Row[]> {
const index = new Map<string, Row[]>();\
for (const row of rows) {
for (const column of columns) {
const cell = column.render(row).toLowerCase();
let rows = index.get(cell);
if (rows == null) {
rows = [];
index.set(cell, rows);
}
rows.push(row);
}
}
return index;
}
Then, we need a search function that iterates our new index:
function searchIndex(
rows: Row[],
index: Map<string, Row[]>,
term: string,
): Row[] {
// A row may have generated more than one cell that
// matches this search term, so we deduplicate with a Set.
const matches = new Set();
for (const [cell, rows] of index) {
if (cell.includes(term)) {
for (const row of rows) {
matches.add(row);
}
}
}
// retain input sort order
return rows.filter((row) => matches.has(row));
}
How does this compare to our original search function?
377ms basicSearch()
192ms searchIndex()
Much better! We are already almost 2x faster, and this is only our first attempt!
We’ll examine the cost of constructing this index later. For now, let’s see how far we can take search performane. Inside searchIndex(), we are doing a few repetitive operations:
Map.iteratevia the first loopstring.includesinside the first loopSet.addinside the second loopSet.hasduringrows.filter
Can we improve any of these operations?
Improving Map.iterate
Internally, Map.iterate this invokes the Javascript iteration protocol, which constructs an object that implements the protocol by defining several properties. This means the first for loop is creating an object for each unique cell, or 656,796 times in our example dataset. Creating that many objects is not only expensive in CPU time, but also in memory usage, and later in garbage collection (adding yet more CPU load).
What if we try generating an index we can iterate without the overhead of Javascript’s iteration protocol?
First, we’ll modify prepareIndex to return parallel arrays instead of a map.
function prepareIndex(
columns: Column[],
rows: Row[],
): [string[], Row[][]] {
const index = new Map<string, Row[]>();
for (const row of rows) {
for (const column of columns) {
const cell = column.render(row).toLowerCase();
let rows = index.get(cell);
if (rows == null) {
rows = [];
index.set(cell, rows);
}
rows.push(row);
}
}
return [Array.from(index.keys()), Array.from(index.values())];
}
Then we’ll modify searchIndex to iterate the parallel arrays instead of the map:
function searchIndexOfRowsViaParallelArrays(
rows: Row[],
[cells, rows]: [string[], Row[][]],
term: string,
): Row[] {
const matches = new Set();
for (let i = 0; i < cells.length; ++i) {
if (cells[i].includes(term)) {
for (let row of rowsArray[i]) {
matches.add(row);
}
}
}
return rows.filter((row) => matches.has(row));
}
How does this new function do?
377ms basicSearch()
192ms searchIndex()
171ms searchIndex() via parallel arrays
Not a huge improvement, but it’s definitely better. What if we try improving the Set operations?
Improving Set.add and Set.has
Internally, a Set is a hash table. Unlike arrays, hash tables have constant-time add and has operations and constant-time merge deduplication, so they are well-suited to the new search implementation.
The v8 team wrote an excellent blog post with a deep dive on the performance characteristics of hash tables in v8, the Javascript engine powering Chrome. You should read it! One of my takeaways is is that hashing objects is complicated. Before v8’s hash tables can operate on an object, v8 generates a random number and stores that number in an internal slot on the object. Hash tables then retrieve that number when they need to determine an object’s hash – for instance, during Set.add or Set.has.
v8 has to do a lot of work to generate, store, and retrieve a number that represents each row. But it turns out we already have a number that represents each row: its array index! If we stored the array index instead of the row in our Set, then theoretically v8 will need to do less work. Hopefully it won’t have to generate/store/retrieve numbers if we’re already giving it one.
In theory, at least. What do the numbers actually look like in practice?
function prepareIndex(
columns: Column[],
rows: Row[],
): [string[], number[][]] {
const index = new Map<string, number[]>();
for (const row of rows) {
for (const column of columns) {
const cell = column.render(row).toLowerCase();
let rows = index.get(cell);
if (rows == null) {
rows = [];
index.set(cell, rows);
}
rows.push(i);
}
}
return [Array.from(index.keys()), Array.from(index.values())];
}
Just a simple change to prepareIndex and searchIndex to operate on row array indexes instead of the rows themselves…
function searchIndex(
rows: Row[],
[cells, rows]: [string[], number[][]],
term: string,
): Row[] {
const matches = new Set();
for (let i = 0; i < cells.length; ++i) {
if (cells[i].includes(term)) {
for (let row of rowsArray[i]) {
matches.add(row);
}
}
}
return rows.filter((row, i) => matches.has(i));
}
Looking good! How does it do?
377ms basicSearch()
192ms searchIndex()
171ms searchIndex() via parallel arrays
106ms searchIndex() with Set<number>
Nice! Another big win! Unfortunately, we’re still outside our 50ms budget, and finding search matches is only half the problem. After we find the search matches, our UI framework still needs to render or rerender matching components. On a large table, this involves an amount of shuffling proportional to the number of search matches – 297,616 in our example. We want to give our UI framework plenty of time to deal with the results of our search operation, meaning the we want to spend as little of our performance budget as possible finding search matches. Can we do better?
Representing a Set of Numbers
A set of numbers can be represented in a few different ways. A hash table is one way, but it is not the most efficient way. What if we use a type of set that is well-suited to numbers? I went searching and found Daniel Lemire’s FastBitSet. It implements the same add/has API as a vanilla Javascript Set, but instead of using a hash table, it represents each number as a single bit in an array of bytes. This kind of data structure is perfectly suited to a list of small, contiguous integers. What if we try using a BitSet instead of a Set?
function searchIndex(
rows: Row[],
[cells, rows]: [string[], number[][]],
term: string,
): Row[] {
const matches = new BitSet();
for (let i = 0; i < cells.length; ++i) {
if (cells[i].includes(term)) {
for (let row of rowsArray[i]) {
matches.add(row);
}
}
}
return rows.filter((row, i) => matches.has(i));
}
Since BitSet has the same API as Set<number>, this change is a one-liner. Cool! How does it perform?
377ms basicSearch()
192ms searchIndex()
171ms searchIndex() via parallel arrays
106ms searchIndex() with Set<number>
46ms searchIndex() with BitSet
Oh baby! Over two times faster than a generic Set, and almost 10x faster than our starting point! Really goes to show the effect the right data structure can have on performance!
The BitSet also gives us access to another optimization. A BitSet can be efficiently converted to an integer array ordered from 0 to n, meaning these two operations do the same thing:
// These two operations give the same results
rows.filter((row, i) => matches.has(i));
matches.array().map((i) => rows[i]);
In the latter case, we are iterating only the matches instead of the entire dataset. What does that change do for us?
377ms basicSearch()
192ms searchIndex()
171ms searchIndex() via parallel arrays
106ms searchIndex() with Set<number>
46ms searchIndex() with BitSet
42ms searchIndex() iterating matches only
The difference isn’t significant when the search term is short and there are large numbers of search results. But as the search term grows longer and the search results shrink, iterating only the matches becomes a much faster operation than iterating the entire dataset. If we use a longer search term for testing, the difference really starts to show. (Our longer search term still matches tens of thousands of rows.)
377ms basicSearch()
192ms searchIndex()
171ms searchIndex() via parallel arrays
106ms searchIndex() with Set<number>
46ms searchIndex() with BitSet
42ms searchIndex() iterating matches only
28ms searchIndex() with a long search term
Nice! Our search gets faster as the search term gets longer!
Evaluating Our Progress
At this point, we have a decision to make. Our new search operation is within our 50ms budget. Is that good enough?
To answer that question thoroughly, we also need to tackle another measurement we haven’t considered yet: the cost of constructing the index. Our current index consumes 332MB of memory and requires 2800ms to create. That’s three seconds of waiting before we can even begin our search operation. Fortunately, we can use some UI tricks2 to hide the cost of constructing the index. Tricks can only take us so far – but it’s definitely possible to hide the waiting time behind a UI smokescreen without the user really feeling the delay.
At this point, we are constructing an index over a million unique cells in 3 seconds, and this index enables sub-50ms searches. In our application, those numbers are absolutely within acceptable limits, with some room to spare as dataset sizes continue to increase.
So we can stop here, right? Well, yeah, we can!
For fun, we could go on to explore more advanced indexing algorithms. Our current indexing strategy still requires us to call string.includes across every unique cell in the table. A suffix tree, for example, would eliminate the need to call string.includes entirely – at the expense of significant time and memory to construct. But our current indexing strategy, though simple and humble, meets our requirements, and so we’ll stop there for today.
-
All tests were performed on an Apple M1 Pro with 32GB of RAM. ↩
-
In our application, the user experience requires the user to click a Search button before the search field appears. We initiate the index construction as soon as the user clicks the Search button. Often, by the time your hands move from your mouse to your keyboard, a good chunk of the index has already been constructed. The user never really feels the time gap to construct the index because it happens in between other actions. If the index required more time to create, we could also split the work into batches and execute each batch during browser idle time using something like
requestIdleCallback. Obviously, these tricks become less effective as the index construction becomes more expensive though. ↩